Godel - Định lý Bất toàn (Incompleteness Theorems)

Chúng ta thường nghĩ: “Nếu nó đúng, nó phải chứng minh được.” Kurt Gödel nói: “Sai rồi.”

Định lý Bất toàn (Incompleteness Theorems) là cú tát mạnh mẽ vào tham vọng của con người muốn đóng gói toàn bộ toán học vào một hệ thống hoàn hảo. Gödel đã chỉ ra rằng trong bất kỳ hệ thống toán học đủ phức tạp nào, sẽ luôn tồn tại những mệnh đề ĐÚNG nhưng KHÔNG THỂ CHỨNG MINH được trong hệ thống đó.

Giáo sư Joel David Hamkins giải thích điều này một cách tài tình thông qua sự phân biệt giữa Ngữ nghĩa (Semantics - Truth) và Cú pháp (Syntax - Proof).

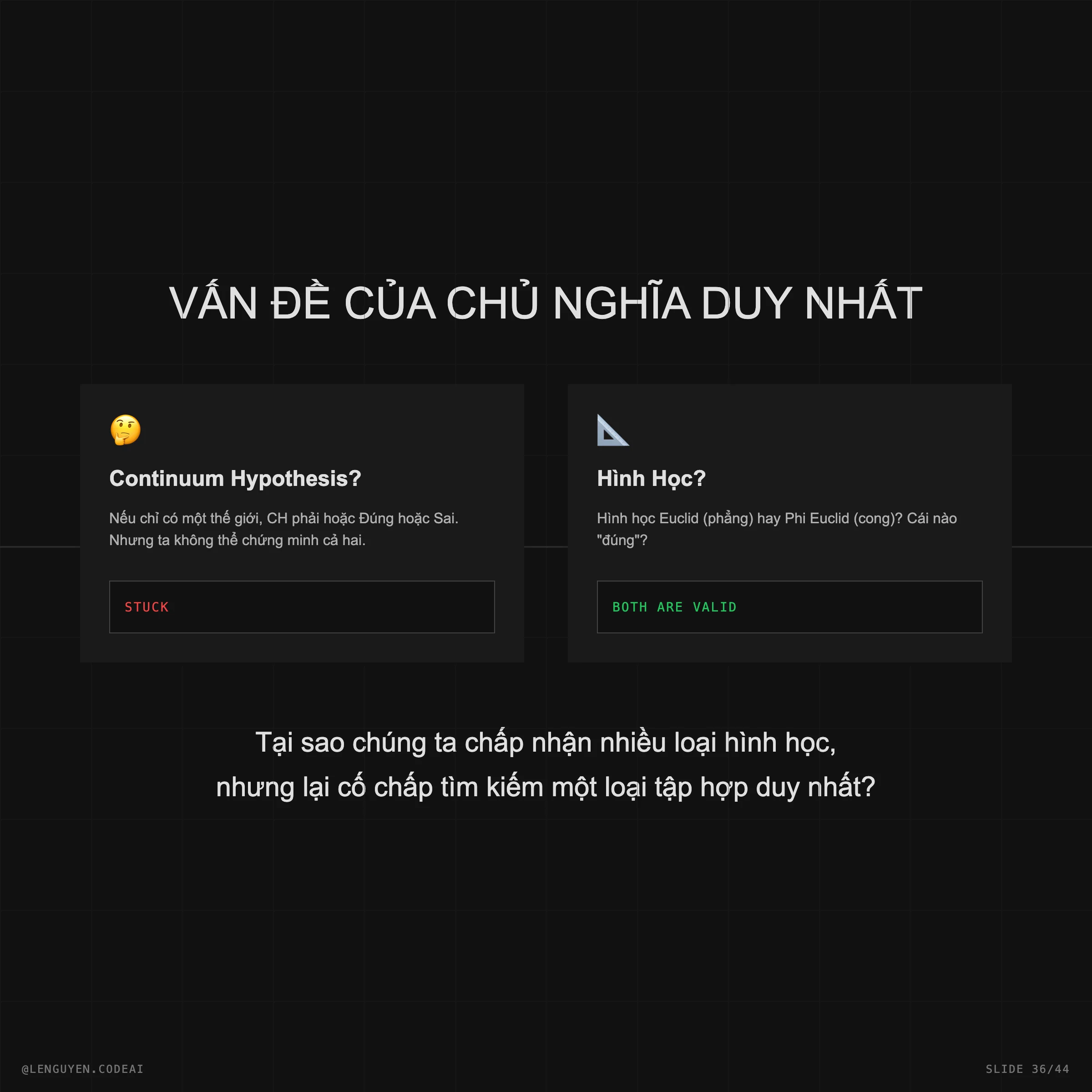
• Truth (Sự thật): Liên quan đến bản chất của thực tại toán học (Platonic realm).
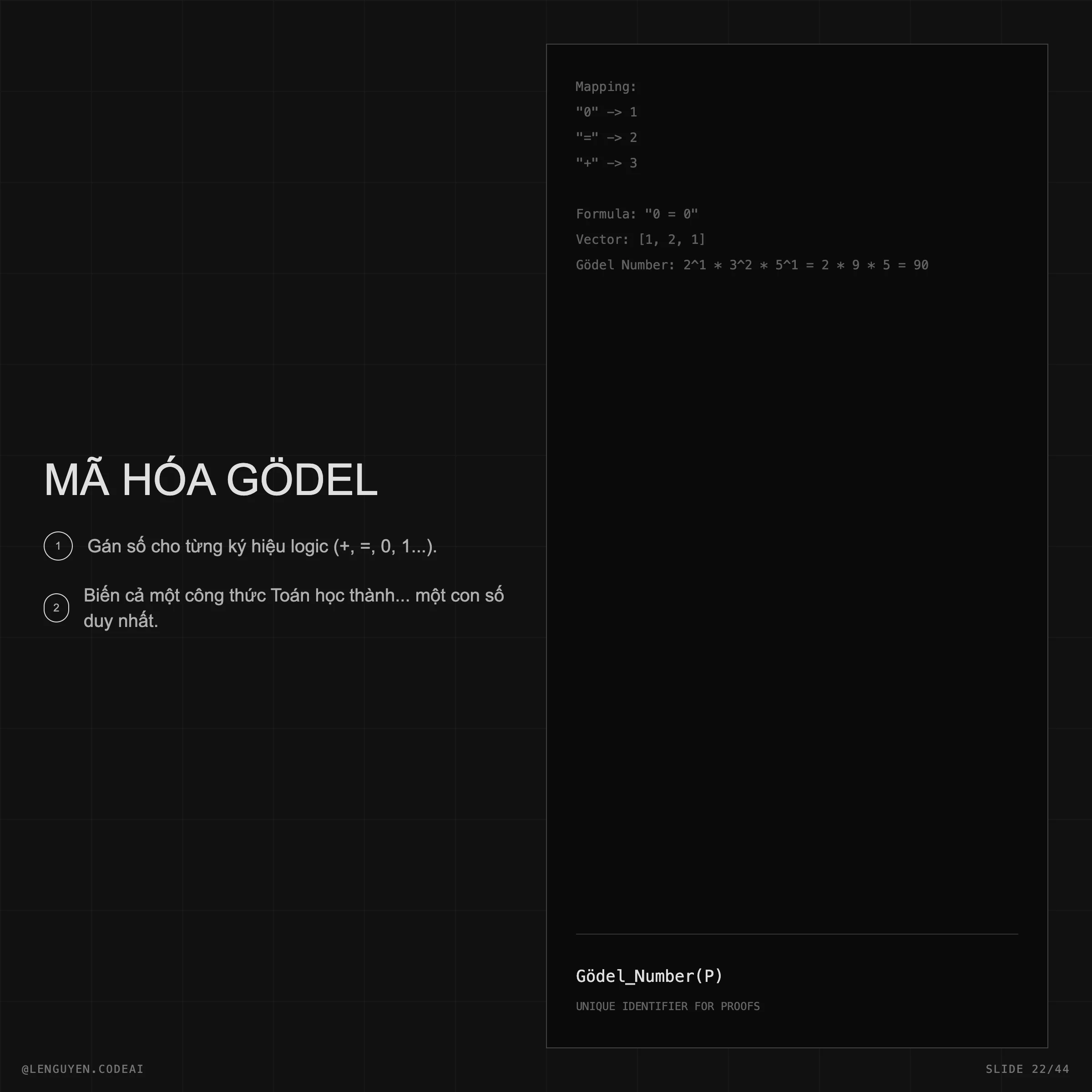
• Proof (Chứng minh): Chỉ là một trò chơi thao tác các ký hiệu hữu hạn.

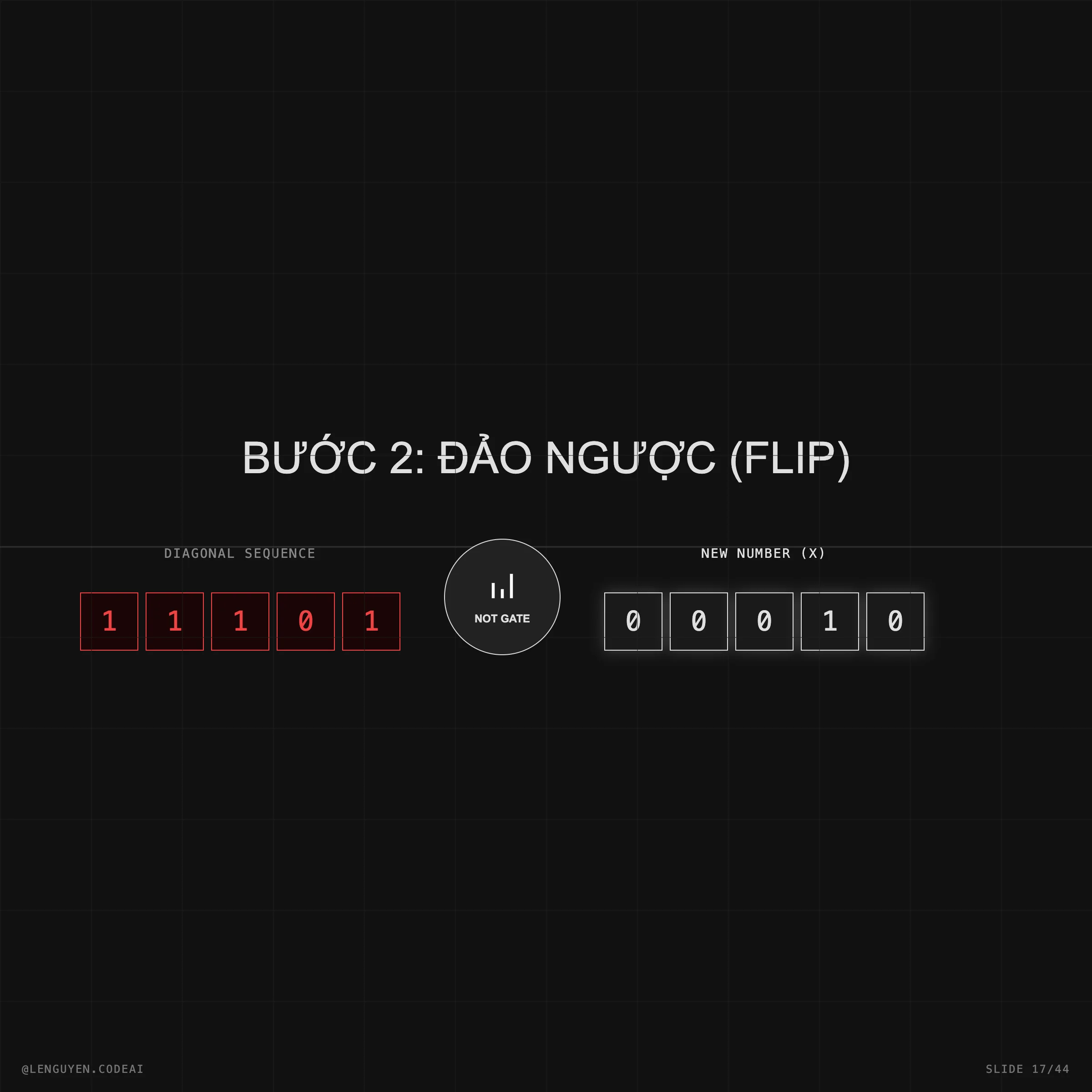
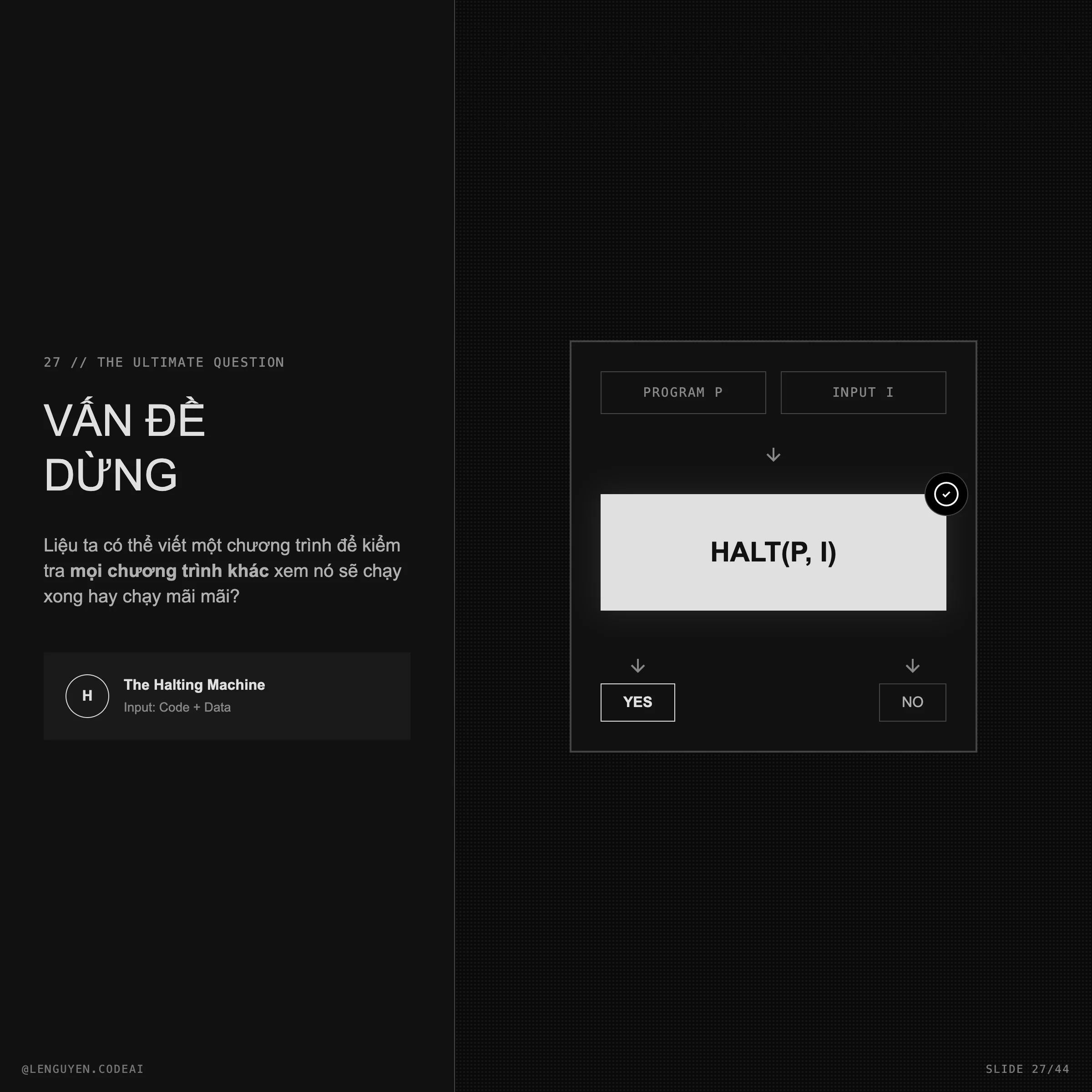
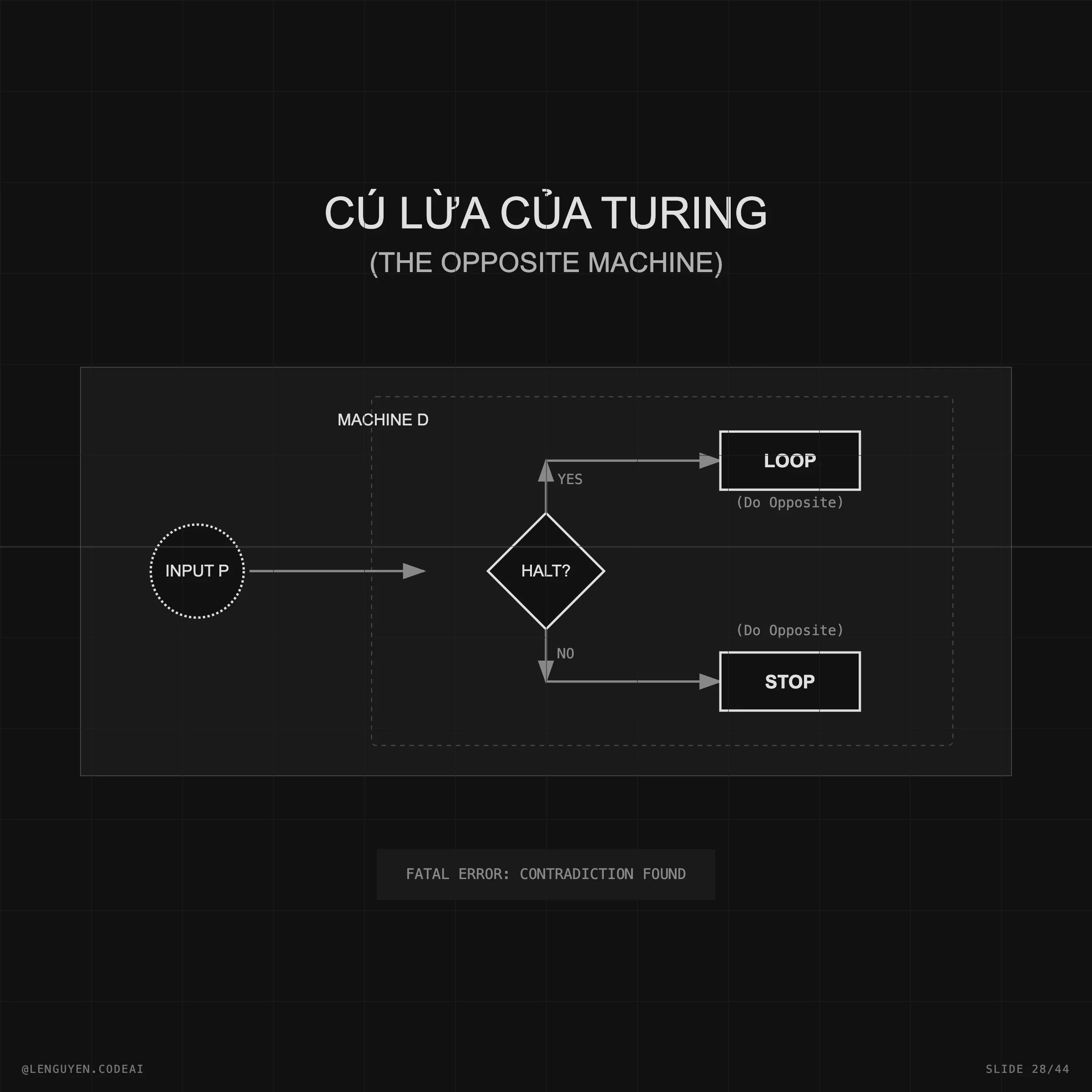
Nếu bạn là dân lập trình, bạn sẽ thấy sự tương đồng rùng mình với Halting Problem của Alan Turing. Hóa ra, giới hạn của tính toán và giới hạn của toán học là hai mặt của một đồng xu.

Một bài viết dành cho những ai thích “hack não” và suy ngẫm về giới hạn của tri thức nhân loại.